Answer:
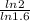 , or ~1.4747
, or ~1.4747
 . You didn't specify a unit for t, so if that is days, months, or years, that is the amount of specified time.
. You didn't specify a unit for t, so if that is days, months, or years, that is the amount of specified time.
Explanation:
To calculate how long it will take to double, you need to solve for the variable
 .
.
To do this, insert the doubled value of 500 where
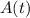 currently is.
currently is.
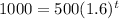
Then, simplify the equation by dividing each side by 500.
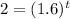
Then, take the logarithm of both sides.
㏑2 = ㏑(1.6)^t
Using the rule of logarithms, you can simplify this further:
㏑2 = t * ㏑1.6
Next, you can divide each side by ㏑1.6. This is your final answer.
You can simplify this further by dividing the logarithms.