Answer:
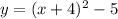
Explanation:
Finding the equation of a translated graph is simple with quadratic equations.
It's easier to use vertex form for this.
Vertex form is shown as the following:
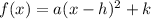
The coordinates (h, k) are the vertex of the parabola. In this case, the new vertex is (-4, -5).
We can plug those in like this:
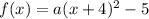
The "a" at the beginning of the equation is used to show how steep/flat the equation is. The only thing that was done to the graph in this case was translation, so this step is not necessary.