Question

Simplify 42+7a using the distributive property

Answer 1

Hey there!

Note:

This expression is already simplified using the Distributive Property. So in order to simplify this expression, we need to factor.

Factoring is the opposite of distributing:

Distributing looks like so:

a(b+c)=ab+ac

So we have a term a and we distribute it by multiplying it times b and c; a, b, and c can be either constants or variables (constants are numbers, and variables are letters, or we can have both numbers and variables in a term - in that case, numbers are called coefficients)

That's why this property is called "The Distributive Property" because we take a term outside the parentheses and distribute it.

Factoring looks like so:

ab+ac=a(b+c)

Instead of multiplying times the common term, we divide by the common term.

And factoring is exactly what we should do here.

We have

`\hookrightarrow\sf{42+7a}`

What is the Greatest Common Factor? That's right, 7.

In order to factor it out, we should divide the entire binomial (a polynomial with 2 terms) by 7.

This is what we get:

`\hookrightarrow\sf{7(6+a)}`

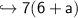
Are we able to simplify this expression any further? No, because 6 and a aren't like terms.

Hope everything is clear.

Let me know if you have any questions!

#KeepOnLearningWithJoy

`\boxed{An~Emotional~Helper~Willing~To~Assist~Others}`

Answer 2

7(6 + a)

General Formulas and Concepts:

Algebra I

• Factoring

Explanation:

Step 1: Define

42 + 7a

Step 2: Simplify

1. Factor out GCF (7): 7(6 + a)