Question

Kathy and her brother Clay recently ran in a local marathon. The distribution of finishing time for women was approximately normal with mean 259 minutes and standard deviation 32 minutes. The distribution of finishing time for men was approximately normal with mean 242 minutes and standard deviation 29 minutes.

(a) The finishing time for Clay was 289 minutes. Calculate and interpret the standardized score for Clay’s marathon time. Show your work.

(b) The finishing time for Kathy was 272 minutes. What proportion of women who ran the marathon had a finishing time less than Kathy’s? Show your work.

(c) The standard deviation of finishing time is greater for women than for men. What does this indicate about the finishing times of the women who ran the marathon compared to the finishing times of the men who ran the marathon?

Answer 1

a) Clay's marathon time is 1.62 standard deviations above the mean finishing time for men.

b) 69.51% of those who ran the marathon has a finishing time less than 272.

c) The spread in the distribution of women's finishing time is greater as compared to the spread in the distribution of men's finishing time.

Explanation:

Part a) It was given that, the finishing time for Clay's marathon time is 289 minutes.

To calculate the standardized test score for Clay's marathon time, we use the formula:

`z = (x - \mu)/( \sigma)`

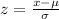
where

`x = 289`

`\mu = 242`

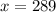
and

`\sigma = 29`

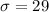
We substitute the values into the formula to get:

`z = (289 - 242)/(29) = 1.62`

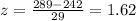
Interpretation: Clay's marathon time is 1.62 standard deviations above the mean finishing time for men.

b) To calculate the proportion of women that had a finishing time less than Kathy , we again need to calculate the z-score for x=272, with mean for women being 259 minutes and standard deviation 32 minutes.

We substitute to get:

`z = (272 - 259)/(32) = 0.41`

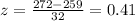
From the standard normal distribution table, P(z<0.41)=0.6951

Therefore 69.51% of those who ran the marathon has a finishing time less than 272.

c) The standard deviation measures the variation of a distribution. This means the standard deviation measures how far away the data set of a distribution are from the mean.

If the standard deviation of finishing time is greater for women than for men, then it indicates that, women's finishing time are far away from the mean finishing time as compared to men's finishing time.