Question

Please help me with the Square Root problems, Part 4. Please Show and Check the work.


`13. x + 2 = 4√(x-2) \\\\14. √(2x-1) +√(3x-12) = 0\\\\15. x = 2√(x-4) + 4\\\\16. x-2= √(9x-36)`

Answer 1

13. x = 6

14. No real solutions

15. x = 4, 8

16. x = 5, 8

Explanation:

13. Square both sides

(x + 2)² = 4²(x - 2)

x² + 4x + 4 = 16x - 32

x² - 12x + 36 = 0

x² - 6x - 6x + 36 = 0

x(x - 6) - 6(x - 6) = 0

(x - 6)(x - 6) = 0

x = 6

14. sqrt(2x - 1) = -sqrt(3x - 12)

No real solutions because a positive square root can not be equal to a negative square root

15. x - 4 = 2sqrt(x - 4)

(x - 4)² = 4(x - 4)

(x - 4)² - 4(x - 4) = 0

(x - 4)(x - 4 - 4) = 0

(x - 4)(x - 8) = 0

x = 4, 8

16. x - 2 = sqrt(9x - 36)

(x - 2)² = (9x - 36)

x² - 4x + 4 - 9x + 36 = 0

x² - 13x + 40 = 0

x² - 5x - 8x + 40 = 0

x(x - 5) - 8(x - 5) = 0

(x - 8)(x - 5) = 0

x = 5, 8

Answer 2

Answers and Step-by-step explanations

13. Square both sides: x^2 + 4x + 4 = 16(x - 2) = 16x - 32

Move all the terms to one side: x^2 - 12x + 36 = 0

Factorize: (x - 6)^2 = 0 ⇒ x = 6

14. Move one of the roots to one side:
`-√(2x-1) =√(3x-12)`

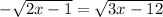
Square both sides: 2x - 1 = 3x - 12

Solve for x: x = 11

15. Subtract 4 from both sides: x - 4 =
`2√(x-4)`

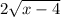
Square both sides: x^2 - 8x + 16 = 4(x - 4) = 4x - 16

Move all the terms to one side: x^2 - 12x + 32 = 0

Factorize: (x - 4)(x - 8) = 0 ⇒ x = 4 or x = 8

16. Square both sides: x^2 - 4x + 4 = 9x - 36

Move all the terms to one side: x^2 - 13x + 40 = 0

Factorize: (x - 5)(x - 8) = 0 ⇒ x = 5 or x = 8

Hope this helps!