Answer:
Given inequality:
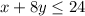
Part A
Solid line: ≤ or ≥
Dashed line: < or >
Therefore, the line will be solid.
Part B
Shading above the line: y > or y ≥
Shading below the line: y < or y ≤
Therefore, shade below the line.
Part C
Make y the subject to determine where to shade.
Given inequality:
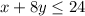
Subtract x from both sides:
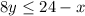
Divide both sides by 8:
