Question

Please help me with the Square Root problems, Part 3. Please Show and Check the work.


`9. √(x+12) +√(x) = 6\\\\10. 2√(x) = 1 - √(4x-1) \\\\11. 2x = √(4x-1) \\\\12. √(4x-1) = 2 - 2x`

Answer 1

9. x = 4

10. x = ¼

11. x = ½

12. x = ½

Explanation:

9. sqrt(x + 12) = 6 - sqrt(x)

Square both sides

x + 12 = 36 - 12sqrt(x) + x

12sqrt(x) = 24

sqrt(x) = 2

x = 4

10. 2sqrt(x) = 1 - sqrt(4x - 1)

Square both sides

4x = 1 - 2sqrt(4x - 1) + 4x - 1

-2sqrt(4x - 1) = 0

sqrt(4x - 1) = 0

4x - 1 = 0

x = ¼

11. 2x = sqrt(4x - 1)

4x² = 4x - 1

4x² - 4x + 1 = 0

4x² - 2x - 2x + 1 = 0

2x(2x - 1) - (2x - 1) = 0

(2x - 1)(2x - 1) = 0

x = ½

12. sqrt(4x - 1) = 2 - 2x

4x - 1 = (2 - 2x)²

4x - 1 = 4 - 8x + 4x²

4x² - 12x + 5 = 0

4x² - 2x - 10x + 5 = 0

2x(2x - 1) - 5(2x + 1) = 0

(2x - 1)(2x - 5) = 0

x = ½ , 5/2

x = 2.5 is rejected because it doesn't satisfy the equation

* when solving equations involving radicals, make sure to verify your answers by plugging in the values in the initial equation

Answer 2

Answers and Step-by-step explanations:

9. Subtract root x from both sides:
`√(x+12) =6-√(x)`

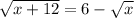
Square both sides: x + 12 = 36 - 12
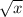`√(x)` + x

Subtract x and 36 from both sides: -24 = -12
`√(x)`

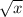
Divide both sides by -12: 2 =
`√(x)`

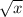
Square both sides again: x = 4

10. Switch the places of the two root expressions:
`√(4x-1) =1-2√(x)`

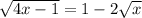
Square both sides: 4x - 1 = 1 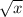- 4
`√(x)` + 4x

Subtract 4x and 1 from both sides: -2 = -4
`√(x)`

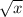
Divide by -4 from both sides: 1/2 =
`√(x)`

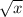
Square both sides again: x = 1/4

11. Square both sides: 4x^2 = 4x - 1

Move all the terms to one side: 4x^2 - 4x + 1 = 0

Factorize: (2x - 1)(2x - 1) = 0 ⇒ x = 1/2

12. Square both sides: 4x - 1 = 4 - 8x + 4x^2

Move all the terms to one side: 4x^2 - 12x + 5 = 0

(2x - 5)(2x - 1) = 0 ⇒ x = 5/2 or x = 1/2

Hope this helps!