Question

A volume of a coin is 113.04 mm2 what is the approximate of a sphere that has the same height and a circular base with the same diameter?Use 3.14 for x round to the nearest hundredth

Answer 1

We have been given that the volume of a cone is 113.04 cubic mm. We are asked to find the approximate volume of a sphere that has the same height and a circular base with the same diameter.

We know that volume of cone is
`(1)/(3)\pi r^2\cdot h`.

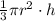The height is equal to the diameter. We know that diameter is 2 times radius, so we can represent this information in an equation as:

`h=2r`

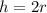
Upon substituting
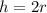`h=2r` in volume of cone, we will get:

`V=(1)/(3)\pi r^2\cdot 2r`

`V=(2)/(3)\pi r^3`

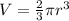
We know that volume of sphere is
`V=(4)/(3)\pi r^3`.

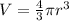Upon comparing volume of cone with volume of sphere, we can see that volume of sphere is 2 times the volume of cone.

`V=2((2)/(3)\pi r^3)`

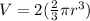
Since
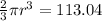`(2)/(3)\pi r^3=113.04`, so volume of sphere would be:

`V=2(113.04)`

`V=226.08`

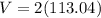
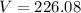
Therefore, volume of sphere would be 226.08 cubic mm.