Answer:
7. x = -2 +/-
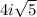
8. x = 2 or x = 6
9. x = -2 +/-
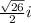
10. t = -3 +/-
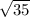
Explanation:
7. Subtract 320 from both sides: 4(x + 2)^2 = -320
Divide by 4: (x + 2)^2 = -80
Square root both sides: x + 2 = +/-
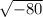 . We need to add the imaginary i to this: +/-
. We need to add the imaginary i to this: +/-
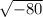 = +/-
= +/-
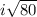 = +/-
= +/-
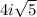
Subtract 2 from both sides: x = -2 +/-
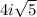
8. Add 18 to both sides: 7(x - 4)^2 = 28
Divide by 7: (x - 4)^2 = 4
Square root both sides: x - 4 = +/- 2
Add 4 to both sides: x = 4 +/- 2 ⇒ x = 2 or x = 6
9. Add 5 to both sides: -2(x + 2)^2 = 13
Divide by -2: (x + 2)^2 = -13/2
Square root both sides: x + 2 = +/-
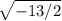 . We again need i: +/-
. We again need i: +/-
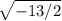 = +/-
= +/-
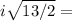 +/-
+/-
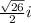
Subtract 2 from both sides: x = -2 +/-
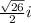
10. Multiply by 5 on both sides: (t + 3)^2 = 35
Square root both sides: t + 3 = +/-
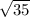
Subtract 3: t = -3 +/-
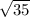
Hope this helps!