Question

What is the value of x?
(geometry question)

Answer 1

Given:

The interior angles of the triangle are 44°, 3t - 45° and x - 15°

The exterior angle of the triangle is 4t - 29°

We need to determine the value of x.

Value of t:

The value of t can be determined using the exterior angle theorem.

Applying the theorem, we have;

`44+3t - 45=4t-29`

`3t - 1=4t-29`

`-t - 1=-29`

`-t=-28`

`t=28`

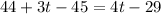
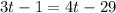
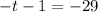
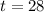
Thus, the value of t is 28.

Value of x:

The exterior angle 4t -29 and the interior angle x - 15 are linear pairs.

Since, linear pairs add up to 180°, we have;

`4t-29+x-15=180`

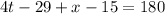
Substituting t = 28, we get;

`4(28)-29+x-15=180`

`112-29+x-15=180`

`x+68=180`

`x=112`

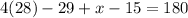
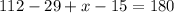
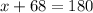
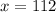
Thus, the value of x is 112.