Question

All members of our painting team paint at the same rate. If $20$ members can paint a $6000$ square foot wall in $24$ minutes, then how long would it take the $20$ members to paint a $9000$ square foot wall, in minutes?

Answer 1

36 minutes

Explanation:

The amount of time needed and the amount of wall to paint are directly proportional. So, when we multiply the amount of wall to paint by 4/3 (going from 6000 square feet to 9000 square feet), we multiply the time needed by 9000/6000 = 3/2. Therefore, the 20 members need 24 * 3/2 = 36 minutes to paint the 9000 square foot wall.

Answer 2

Let x represent time taken by 20 members to paint 9000 square foot wall.

We have been given that all members of our painting team paint at the same rate. 20 members can paint a 6000 square foot wall in 24 minutes. We are asked to find the time taken by 20 members to paint 9000 square foot wall.

We will use proportions to solve our given problem.

`\frac{\text{Time taken}}{\text{Area of wall painted}}=\frac{24\text{ min}}{6000\text{ ft}^2}`

`\frac{x}{9000\text{ ft}^2}=\frac{24\text{ min}}{6000\text{ ft}^2}`

`\frac{x}{9000\text{ ft}^2}* 9000\text{ ft}^2=\frac{24\text{ min}}{6000\text{ ft}^2}* 9000\text{ ft}^2`

`x=\frac{24\text{ min}}{6}* 9`

`x=4\text{ min}* 9`

`x=36\text{ min}`

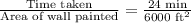
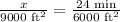
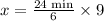
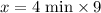
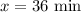
Therefore, it will take 36 minutes for 20 members to paint 9000 square foot wall.