Question

Please assist me with this problem​

Answer 1

a)
`√(64+x^2)`

b) 15

Explanation:

a) We know that AB = 8 and BC = x. We can use the Pythagorean Theorem, which states that for a right triangle with sides a, b, and c:
`a^2 +b^2=c^2` , where a and b are the shortest sides and c is the longest.

Here, AB = a = 8 and BC = b = x. So, AC = c. Then:

`AB^2+BC^2=AC^2`

`8^2+x^2=AC^2`

`AC=√(64+x^2)`

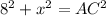
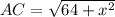
b) We know that AC - AB = 9. Since AB = 8, then AC = 9 + 8 = 17. We also have the expression from above, so set them equal:

`AC=√(64+x^2)=17`

`64+x^2=289`

`x^2=225`

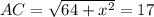
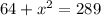
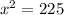
x = 15

Hope this helps!

Answer 2

sqrt(x^2 +64) = AC

x = 15

Explanation:

We can use the Pythagorean theorem since this is a right triangle

a^2 + b^2 =c^2 a and b are the legs and c is the hypotenuse

We know the legs are x and 8

x^2 + 8^2 = AC^2

x^2 + 64= AC^2

Solving for AC

Take the square root of each side

sqrt(x^2 + 64) = sqrt(AC^2)

sqrt(x^2 +64) = AC

We are given AC - AB = 9

We know AB = 8

AC -8 =9

Add 8 to each side

AC -8+8 = 9+8

AC = 17

AC is the hypotenuse,

x^2 + 64= AC^2

x^2 +64 = 17^2

x^2 +64 = 289

Subtract 64 from each side

x^2 +64-64 = 289-64

x^2 =225

Take the square root

sqrt(x^2) = sqrt(225)

x =15