Question

A waterfall has a hit of 1500 ft. A pebble is thrown upward at the velocity of 24ft per second. The hot, h, of the pebble after t seconds is given by the equation h=-16t+24t+1500. How long after the pebble is thrown will it hit the ground.

Answer 1

A waterfall has a height of 1500 feet. A pebble is thrown upward from the top of the falls with an initial velocity of 24 feet per second. The​ height, h, of the pebble after t seconds is given by the equation h =−16t^2+24t+1500. How long after the pebble is thrown will it hit the​ ground?

Pebble will hit the ground after 10.46 seconds.

Explanation:

Given:

The​ height, "h" of the pebble after t seconds, "h" = −16t^2+24t+1500

We have to find the time it will take to hit the ground.

For this we have to put h = 0 and solve the quadratic.

Quadratic formula:

⇒ Standard equation :
`ax^2+bx+c=0`

⇒
`x =(-b\pm √((b)^2-4ac) )/(2a)`

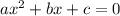
Now,

Solving the above equation with quadratic formula after comparing its values with the standard equation.

⇒
`a=-16,\ b=24,\ c=1500`

⇒
`t =(-b\pm √((b)^2-4ac) )/(2a)`

⇒
`t =(-24\pm √((24)^2-4(-16)(1500)) )/(2(-16))`

⇒
`t =(-24\pm √(576+96,000) )/(-32)`

⇒
`t =(-24\pm(310.76))/(-32)`

⇒
`t =(-24+(310.76))/(-32)` ⇒
`t =(-24-(310.76))/(-32)`

⇒
`t =-(286.76)/(32)` ⇒
`t =(334.76)/(32)`

⇒
`t=-8.96\ sec` ⇒
`t=10.46\ sec`

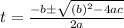
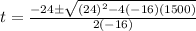
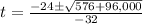
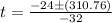
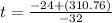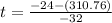
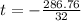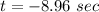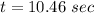
Discarding the negative values.

The pebble will hit the ground after 10.46 seconds.