Question

Un agricultor dispone de 450 m. De valla para cercar un terreno circular de radio r y uno rectangular cuyo lado menor es igual al diámetro del terreno circular. Encuentra la función que da la suma de las áreas de ambos terrenos en función del radio r. ¿Cómo se llama la función resultante? ¿Cómo es su gráfica?

Answer 1

Explanation:

El gráfico de la región está adjunta. En la imagen, d corresponde al gráfico de diámetro del círculo. Sabemos, que tenemos un total de 450 metros de cerca. Luego, el perímetro de nuestra figura es de 450. Sabiendo que el perímetro de un círculo de radio r es
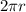`2\pi r`. Tenemos la siguiente ecuación

`\pi \cdot r + 2x + 2r = 450`

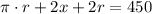
De donde deducimos que

`x = (450-r(\pi+2))/(2)`.

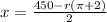Así mismo, sabemos que el área de nuestra figura es la suma del área del rectángulo (base por altura) más el área del semicirculo. Sea f(r) el área de la rigura. Entonces,

`f(r) = (\pi \cdot r^2)/(2)+ 2\cdot r \cdot (450-r(\pi+2))/(2) = (\pi \cdot r^2)/(2)+ r\cdot (450-r(\pi+2))`

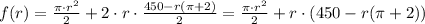
La función es una función cuadrática, ya que es un polinomio de grado 2 para la variable r. Con ayuda de un software de gráficas, podemos ver adjunta la gráfica de la función.