Question

F(x) = x4 + x3 + 2x2 + ax + b,

where a and b are constants.
When f(x) is divided by (x - 1), the remainder is 7
(a) Show that a + b = 3
When f(x) is divided by (x + 2), the remainder is -8
(b) Find the value of a and the value of b

Answer 1

see explanation

Explanation:

The remainder theorem states that if f(x) is divided by (x - h)

The the remainder is f(h)

(a)

Given f(x) is divided by (x - 1) then remainder is f(1), thus

f(1) =
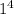`1^(4)` + 1³ + 2(1)² + a + b = 7, that is

1 + 1 + 2 + a + b = 7

4 + a + b = 7 ( subtract 4 from both sides )

a + b = 3 ← as required → (1)

(b

Given f(x) is divided by (x + 2) then the remainder is f(- 2), thus

f(- 2) =
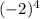`(-2)^(4)` + (- 2)³ + 2(- 2)² + 2a + b = - 8, that is

16 - 8 + 8 + 2a + b = - 8

16 + 2a + b = - 8 ( subtract 16 from both sides )

2a + b = - 24 → (2)

Multiply (1) by 2

2a + 2b = 6 → (3)

Add (2) and (3) term by term to eliminate the term in a

3b = - 18 ( divide both sides by 3 )

b = - 6

Substitute b = - 6 into (1)

a - 6 = 3 ( add 6 to both sides )

a = 9

Thus a = 9 and b = - 6