Question

if an electron in an electron beam experiences a downward force of 2.0x10^-14N while traveling in a magnetic field of 8.3x10^-2T west, what are the direction and the magnitude of the velocity?

Answer 1

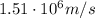`1.51\cdot 10^6 m/s` north

Step-by-step explanation:

When a charged particle moves in a magnetic field, the particle experiences a force given by the formula:

`F=qvB sin \theta`

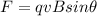
where

q is the magnitude of the charge

v is its velocity

B is the magnetic field

`\theta` is the angle between the directions of v and B

In this problem,

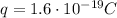`q=1.6\cdot 10^(-19)C` (charge of the electron)

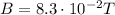`B=8.3\cdot 10^(-2) T` (strength of magnetic field)

`F=2.0\cdot 10^(-14) N` (force)

`\theta=90^(\circ)`

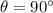
Therefore, the velocity is

`v=(F)/(qB sin \theta)=(2.0\cdot 10^(-14))/((1.6\cdot 10^(-19))(8.3\cdot 10^(-2))(sin 90^(\circ)))=1.51\cdot 10^6 m/s`

The direction of the force is perpendicular to both the direction of the velocity and the magnetic field, and it can be found using the right-hand rule:

. Thumb: direction of the force (downward) --> however the charge is negative, so this direction must be reversed: upward

- Middle finger: direction of the field (west)

- Index finger: direction of velocity --> north

So, the electron is travelling north.