Question

Find the lateral area of a cone.

Answer 1

Answer: B. 1178 cm²

What we are solving for:

The lateral area is, put simply, the surface area of the cone not including the bottom.

The formula is:

L = πr
`\sqrt{h^(2) +r^(2) }`

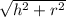
Height of the cone:

This calls for the height, since it is a right triangle we can use the Pythagorean theorem to solve.

a² + b² = c²

15² + b² = 25²

225 + b² = 625

b² = 400

b =
`√(400)`

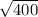
The height is 20 cm

Solving:

Back to the formula,

L = πr
`\sqrt{h^(2) +r^(2) }`

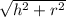
L = π15
`\sqrt{(20)^(2) +(15)^(2) }`

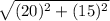
L ≈ 1178.1 cm²

The lateral area of the cone is B. 1,178 cm².