Answer: " x = 1 ± 2i√2 " .
_________________________________
Explanation:
_________________________________
To solve the given equation:
"
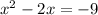 " ;
" ;
for all values of "
 " ; by using the "quadratic formula equation" ;
" ; by using the "quadratic formula equation" ;
we must first rewrite the given equation in "quadratic format" ;
→ that is; in the format:
→ "
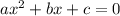 " ; {
" ; {
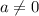 } ;
} ;
________________________________
So, given:
"
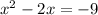 " ;
" ;
→ We must add "9" to Each Side of the equation; to get the equation into "quadratic format" ; as follows:
→ x² − 2x + 9 = -9 + 9 ;
to get:
→ " x² − 2x + 9 = 0 " ;
___________________________________
→ which is written in the "quadratic format" ; that is:
→ "
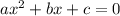 " ; {
" ; {
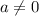 } ;
} ;
in which:
"a = 1" ; [the "implied coefficient; "1" ; since "1" multiplied by "any value" ;
results in "that same value" ;
→ {Note this this is known as the "identity property"
of multiplication.}.
b = -2 ;
c = 9 ;
and since: " a = 1 " ; We know that: " {a≠0.}. "
_______________________________________
To solve for all value(s) for "
 " in our given equation by using the quadratic equation formula:
" in our given equation by using the quadratic equation formula:
→ We use the following quadratic equation formula:
________________________________________
→ x = [-b ± √(b² − 4ac) ] / [2a] ;
Note that in the "quadratic formula" :
→ "
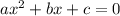 " ; "a ≠ 0" ;
" ; "a ≠ 0" ;
→ Since we divide by "2a" {refer to the "denominator"];
→ and if: "a" were to equal "0" ; then the "denominator" would equal: "2a = 2*a = 2*0 = 0" ; and we cannot divide by "0" .
______________________________________________
So, let us solve for the values for "
 " ; by plugging in our known values into the quadratic equation formula:
" ; by plugging in our known values into the quadratic equation formula:
______________________________________________
→
 = [
= [
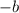 ±
±
![\sqrt{(b^(2)-4ac)} ] / [2a] ;](https://img.qammunity.org/2021/formulas/mathematics/college/12ifnptklt3igaowd1ph4t3zp3bjl83005.png)
So, to solve for "x" ; plug in "1" for "a"; "-2" for "b" ; "9" for "c" ;
→ So: "
 " ;
" ;
" b² = (-2)² = (-2) * (-2) = 4 " ;
" 4ac = 4 * 1 * 9 = 4 * 9 = 36 ;
" 2a = 2 * 1 = 2 " ;
__________________________________________
So:
→ x = (2 ± √(4−36) / 2 ;
Note: 4−36 = -32 ;
So:
→ x = (2 ± √-32) / 2 ;
Note: √-32 ; can be written as " i * √-32" ; or simply: "i√-32" ; since "i" is an 'imaginary number" that can represent the imaginary number: "√-1" ;
→ since: "√-32 = √-1 * √32" ; if: "√-1" really existed.
__________________________________________
→ Now, we can further simplify:
→ i√32;
_________________________________________
Let us simplify: "√32" ;
→ √32 = √16 * √2 = 4 * √2 ; or, write as 4√2 ;
So: √-32 = i√-32 = i * 4√2 = 4i√2 .
_________________________________________
We have, from above:
→ x = (2 ± √-32) / 2 ;
Rewrite—by substituting "4i√2" ; in lieu of: "√-32" ; as following
→ x = (2 ± 4i√2) / 2 ;
We are dividing the numerator by "2" ; so we can further simplify:
to get:
________________________________________
→ " x = 1 ± 2i√2 " .
________________________________________
Hope this answer—and explanation—is helpful!
Wishing you well in your academic endeavors!
________________________________________