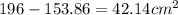Question

Please help!

Two semicircles are placed in a rectangle. The width of the rectangle is 7 cm.

Find the area of the shaded region. Use the value 3.14 for pi , and do not round your answer.

Answer 1

Answer: 42.14
`cm^2`

Explanation:

Assuming that the width of the rectangle is 7 cm, the semi-circle's radius is also 7 cm.

Let's calculate the area of the two semi-circles, which in total makes a whole circle.

The formula for a circle is
`a=2\pi r^2`

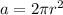
Since r = 7, plug it in the formula:

`a=2\pi (7)^2`

`a=49\pi =153.86 cm^2`

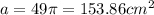
Now, to figure out the length of the rectangle, look at the semi-circles. Their radius is 7 cm, so their diameter is 14 cm. We have two semi-circles with the diameter (14 cm), so we can say that the width is 28 cm.

Area of a rectangle:
`a=lw`

`a=7*28=196cm^2`

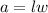
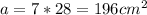
To find the area of the shaded region, we subtract the area of the semi-circles to the rectangle, which should be:

`196 - 153.86=42.14 cm^2`

Answer 2

Total length of the rectangle = 14+14= 28cm

width= 7 cm

Area of the rectangle = 28×7cm²

= 196 cm²

Area of 2 semicircles = Area of 1 circle

= π(7)² = 3.14×49= 153.86cm²

Area of the shaded region = 196-153.86

= 42.14 cm²