Answer:
The change in the cone produces a greater increase in volume.
Explanation:
Let's start with the cone.
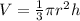
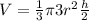 (In your case, you would type V = 1/3pi3r^2h/2)
(In your case, you would type V = 1/3pi3r^2h/2)
The changes that occurred are
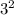 and
and
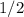 . When we add these together we get
. When we add these together we get
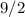 .
.
Now the cylinder.
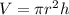
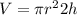 (In your case, you would type V = pir^2 2h)
(In your case, you would type V = pir^2 2h)
The change that occurred is
 .
.
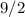 is greater than
is greater than
 which means that the change in the cone produces a greater increase in volume.
which means that the change in the cone produces a greater increase in volume.