Answer:
8)
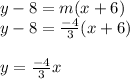
9)
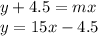
10)
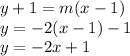
Explanation:
We can use the definition of a line:

where
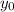 and
and
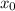 co-ordinates of a point on that line, and where
co-ordinates of a point on that line, and where
 is the gradient of the line.
is the gradient of the line.
We can work out the gradient of the line by looking at the differential, or the change in y compared to the change in x.
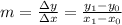
where
 and
and
 are two distinct points on the line.
are two distinct points on the line.
You now have the tools needed to go about answering these questions!