Question

The height of a cylinder is 10 and the area of a base is 36 pi square units. What

is the volume in cubic units

Answer 1

1130.97336 units^3

Explanation:

Answer 2

1130.97336 units^3

Explanation:

The volume of a cylinder can be found using:

`v=\pi r^2h`

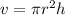
We have the area of the base, but not the radius

`a=\pi r^2`

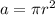
We know the area is
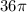`36\pi`, so we can substitute that in for a

`36\pi =\pi r^2`

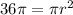
We want to find r, so we need to isolate it

Divide both sides by pi

36=r^2

Take the square root of both sides

6=r

Now we know the radius, and can substitute it into the volume formula, and we can substitute the height (10) in

`v=\pi r^2h`

`v=\pi 6^210`

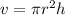
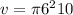
Solve the exponent

`v=\pi 36(10)`

`v=\pi 360`

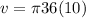
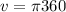
v=1130.97336

The volume is 1130.97336 units^3