Question

What are the lengths of sides A and B of a right triangle if the hypotenuse is equal to 1.2 cm and the interior angles are 60 degrees, 30 degrees, and 90 degrees?

Answer 1

We have been given that the hypotenuse of a right triangle is equal to 1.2 cm and the interior angles are 60 degrees, 30 degrees, and 90 degrees.

We know that hypotenuse corresponds to 90 degrees angles.

We also know that the hypotenuse is equal to twice the length of the shorter leg and shorter leg is the opposite side to 30 degree angle.

To find the length of shorter leg, we will divide length of hypotenuse by 2.

`\text{Side corresponding to 30 degree angle}=\frac{1.2\text{ cm}}{2}`

`\text{Side corresponding to 30 degree angle}=0.6\text{ cm}`

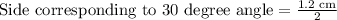
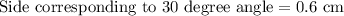
Therefore, length of shorter leg is 0.6 cm.

We know that the longer leg, which is across from the 60 degree angle, is equal to multiplying the shorter leg by
`√(3)`.

`\text{Side corresponding to 60 degree angle}=0.6\text{ cm}* √(3)`

`\text{Side corresponding to 60 degree angle}=1.039230\text{ cm}`

`\text{Side corresponding to 60 degree angle}\approx 1.04\text{ cm}`

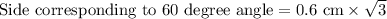
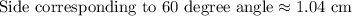
Therefore, length of longer leg is approximately 01.04 cm.