Question

In a study of the accuracy of fast food​ drive-through orders, one restaurant had 36 orders that were not accurate among 324 orders observed. Use a 0.01 significance level to test the claim that the rate of inaccurate orders is equal to​ 10%. Does the accuracy rate appear to be​ acceptable?

Identify the null and alternative hypotheses for this test. Choose the correct answer below.

Answer 1

We do not have sufficient evidence to reject the claim that ,the rate of inaccurate orders is equal to​ 10%.

Explanation:

We want to use a 0.01 significance level to test the claim that the rate of inaccurate orders is equal to​ 10%.

We set up our hypothesis to get:

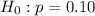`H_0:p=0.10`------->null hypothesis

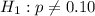`H_1:p\\e0.10`------>alternate hypothesis

This means that:
`p_0=0.10`

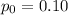
Also, we have that, one restaurant had 36 orders that were not accurate among 324 orders observed.

This implies that:
`\hat p=(36)/(324)=0.11`

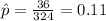
The test statistics is given by:

`z=\frac{\hat p-p_0}{\sqrt{(p_0(1-p_0))/(n) } }`

We substitute to obtain:

`z=\frac{0.11-0.1}{\sqrt{(0.1(1-0.1))/(324) } }`

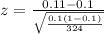
This simplifies to:

`z=0.6`

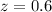
We need to calculate our p-value.

P(z>0.6)=0.2743

Since this is a two tailed test, we multiply the probability by:

The p-value is 2(0.2723)=0.5486

Since the significance level is less than the p-value, we fail to reject the null hypothesis.

We do not have sufficient evidence to reject the claim that ,the rate of inaccurate orders is equal to​ 10%.