Question

16.3: Filling the Sandbox Worksheet.

The daycare has two sandboxes that are both prisms with regular hexagons as their bases. The smaller sandbox has a base area of 1,146 in2 and is filled 10 inches deep with sand.
1. It took 14 bags of sand to fill the small sandbox to this depth. What volume of sand comes in one bag? (Round to the nearest whole cubic inch.)
2. The daycare manager wants to add 3 more inches to the depth of the sand in the small sandbox. How many bags of sand will they need to buy?
3. The daycare manager also wants to add 3 more inches to the depth of the sand in the large sandbox. The base of the large sandbox is a scaled copy of the base of the small sandbox, with a scale factor of 1.5. How many bags of sand will they need to buy for the large sandbox?
4. A lawn and garden store is selling 6 bags of sand for $19.50. How much will they spend to buy all the new sand for both sandboxes?

Answer 1

`1)\ \ 819\ in^3\\\\2)\ \ 19\ bags\\\\3)\ \ 41\ bags\\\\4)\ \ \$195.00`

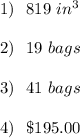
Explanation:

1. Volume of a hexagonal prism is given by the product of the hexagonal base by its height:

`V=bh, b=Base \ Area\\\\=1146* 10\\\\=11460\ in^3`

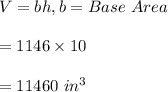
-Given that 14 bags are required to fill the box to this height, we divide the volume calculated above by the number of bags:

`V_(bag)=(V_(prism))/(No \ of \ Bags)\\\\=(11460)/(14)\\\\=818.57\approx819\ in^3`

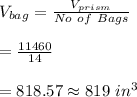
Hence, the volume of each bag is approximately
`819 \ in^3`

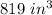
2. If the small box is filled to a depth of 13 inches(depth increases by 3 inches), it's new volume will be:

`V_(prism)=bh\\\\=1146* 13\\\\=14898\ in^3`

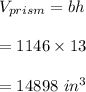
-To find the number of bags needed, we divide the prism's new volume by the volume of each bag:

`V_(prism)=14898\ in^3\\V_(bag)=819\ in^3\\\\No\ of \ Bags=(V_(prism))/(V_(bag))\\\\=(14898)/(819)\\\\=18.19\approx 19\ bags`

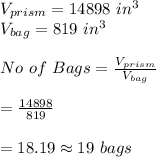
Hence, the daycare has to buy 19 bags of sand.

3 Given the scale factor is 1.5, then the base area of the large sandbox is given by the formula:

`A_(large)=A_(small)*(sf)^2, sf=scale \ factor\\\\A_(large)=1146* 1.5^2\\\\=2578.5\ in^2`

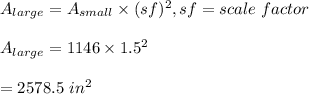
-Assume the large box is filled to the same depth as the small sandbox:

`V=bh, b=2578\ in^2, h=13\ in\\\\\therefore V=2578.5\ * 13\\\\=33,520.5\ in^3`

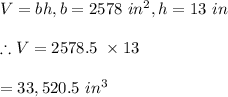
We divide this volume by the volume of each sandbag to get the number of bags to fill the large sandbox:

`No \ of \ \ Bags=(V_(box))/(V_(bag))\\\\=(33520.5)/(819)\\\\\\=40.9286\approx41\ bags`

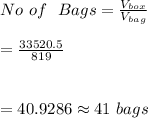
4. The total cost is spent on sand is calculated by multiplying the price of a sand bag by the number of sand bags:

Let X be the cost spent on all the sand bags:

`Bags=41+19=60\ bags\\\\6\ bags=\$19.50\\60\ bags=X\\\\\therefore X=(60\ bags* \$19.50)/(6\ bags)\\\\=\$195.00`

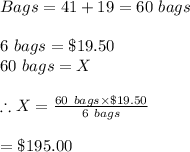
Hence, the total cost of sand is $195.00