Question

Suppose your new business made a profit during the first year of $3000. If the profit increased 12% per year, find the total of all profit earned by the end of the first 5 years.

Answer 1

Therefore the total of all profit earned by the end of of the the first 5 years is $19,058.542.

Explanation:

To find total profit earned per year, we need to use the compound growth formula.

The compound growth formula:

`A= P(1+r)^t`

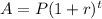
A= Amount after t years

P= initial amount

r= rate of growth

t= time in year.

Given that,

New business made a profit during the first year of $3000.

If the profit increased 12% per year.

Here P= $3,000 and r =12%=0.12 , t=1 years

Plugging all value in the above formula:

`A=3000(1+0.12)^1`

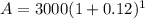
=3000(1.12)

=$3360

Profit after 2 year is $3,360.

Now, P= $3,000 and r =12%=0.12 , t=3 years

`A=3000(1+0.12)^2`

=3000(1.12)²

=$3763.2

Similar the profit at 4 year is

`A=3000(1+0.12)^3`

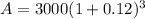
=3000(1.12)³

=$4214.784

The profit at 5th year is

`A=3000(1+0.12)^4`

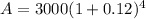
=3000(1.12)⁴

=$4720.558

Therefore the total of all profit earned by the end of of the the first 5 years is=$(3,000+3360+3763.2+4214.784+4720.558)

=$19,058.542