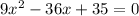Answer:
Option A)
Explanation:
We are given the following in the question:
Roots of quadratic equation are:
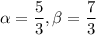
The sum of the roots and the product of the roots can be calculated as:

Standard form of quadratic equation:
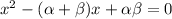
Putting values, we get,
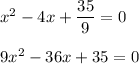
is the required quadratic equation.
Thus, the correct answer is
Option A)