Answer : The partial pressure of
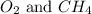 is, 0.281 atm and 0.839 atm respectively.
is, 0.281 atm and 0.839 atm respectively.
The total pressure in vessel is, 1.12 atm.
Explanation :
First we have to calculate the moles of oxygen and methane.
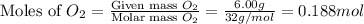
and,
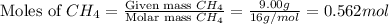
Now we have to calculate the total moles of gas.
Total moles of gas = Moles of oxygen + Moles of methane
Total moles of gas = 0.188 + 0.562
Total moles of gas = 0.75 mol
Now we have to calculate the total pressure of gas by using ideal gas equation.
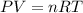
where,
P = total pressure of gas = ?
V = total volume of gas = 15.0 L
n = total number of moles gas = 0.75 mole
R = Gas constant =
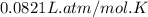
T = Temperature of gas =
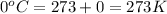
Putting values in above equation, we get:
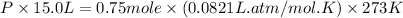
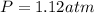
Now we have to calculate the mole fraction of oxygen and methane.
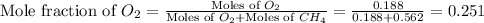
and,
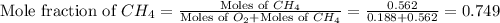
Now we have to calculate the partial pressure of oxygen and methane.
According to the Raoult's law,
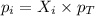
where,
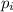 = partial pressure of gas
= partial pressure of gas
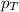 = total pressure of gas = 1.12 atm
= total pressure of gas = 1.12 atm
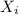 = mole fraction of gas
= mole fraction of gas
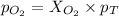
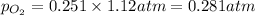
and,
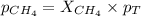
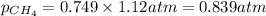
Thus, the partial pressure of
 is, 0.281 atm and 0.839 atm respectively and the total pressure in vessel is, 1.12 atm.
is, 0.281 atm and 0.839 atm respectively and the total pressure in vessel is, 1.12 atm.