Answer:
The height of the cross section if 2 feet
Explanation:
To solve this problem recall the formula for the area of a trapezoid of bases B (larger base) and b (smaller base) and height H:
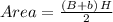
Therefore, for our case we have:
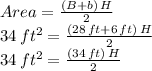
So, now we can solve for the height H:
