Question

Portland's population in 2007 was about 568 thousand, and had been growing by

about 1.1% each year.
a. Write a recursive formula for the population of Portland
b. Write an explicit formula for the population of Portland
c. If this trend continues, what will Portland's population be in 2016?
d. If this trend continues, when will Portland’s population reach 700 thousand?

Answer 1

`a) \ \ P_n=(1+r)P_(n-1)\\\\b)\ \ \ P_n=1.011^n(568000)\\\\c)\ \ 626,771\\\\d)\ \ 19.10yrs\ later \ (2027 \ February)`

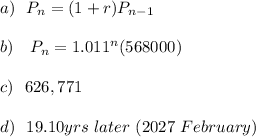
Explanation:

a. Given that the population starts at 568000 and grows at 1.1% each years.

-The recursive formula for the population takes the form:

`P_n=(1+r)P_(n-1)`

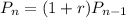
Where:

`P_n` is the population at the nth year.

`r` is the rate of growth

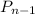`P_(n-1)` is the population a year before the nth year.

Hence, the recursive formula is given by
`P_n=(1+r)P_(n-1)`

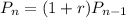
b. The explicit formula of a population growth takes the form:

`P_n=(1+r)^nP_o`

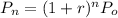
-Given that r=1.1% and the initial population is 568000

`P_n=(1+r)^nP_o\\\\r=1.1\%=0.011\\\\P_n=(1+0.011)^nP_o, P_o=568000\\\\P_n=1.011^n(568000)`

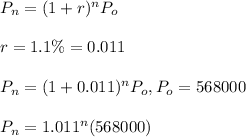
Hence, the explicit formula is
`P_n=1.011^n(568000)`

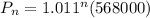
c. The population in 2016 can be determined using the explicit formula.

-We substitute the growth rate and initial population as follows:

`P_n=(1+r)^nP_o\\\\=1.011^n(568000)\\\\n=2016-2007=9\\\\\therefore P_(2016)=(1+0.011)^9* 568000\\\\=626,770.7721\approx626,771`

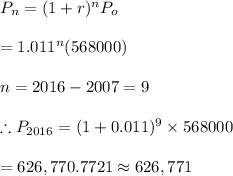
Hence, the population in 2016 will be approximately 626,771

d. Given that the population after n years will be 700000.

#We substitute this value in the explicit formula to solve for n then add it to the initial year, 2007;

`P_n=(1+r)^nP_o\\\\700000=1.011^n(568000)\\\\1.011^n=(700000)/(568000)=(700)/(568)\\\\n=(log \ (700/568))/(log\ 1.011)\\\\=19.10\ years\\\\\#Add \ 19.10yrs \ to \ 2007\\\\=2007+19.10yrs\\\\=2026.10\approx2027`

Hence, the population will get to 700000 after 19.10 years or in February the year 2027