Question

Find the 10th term of the following geometric sequence 6,24,96,384,…

Answer 1

1572864

Explanation:

the nth term of a geoemtric series can be calculated using the following rule :
`a_n=a_1(r)^n^-^1`

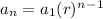
where an = nth term, a1 = first term , r = common ratio and n = term position.

here, the first term is 6, the common ratio is 4 and the term position is 10 ( because we want to find the 10th term )

so a1 = 6 , r = 4 and n = 10

using these values we plug them into the rule

recall rule :
`a_n=a_1(r)^n^-^1`

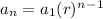
==> plug in a1 = 6 , r = 4 and n - 10

`a_1_0=6(4)^1^0^-^1`

==> subtract 10 and 1

`a_1_0=6(4)^9`

==> simplify exponent

`a_1_0=6(262144)`

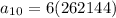
==> simplify multiplication

`a_1_0=1572864`

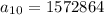
and we are done!

Note:

the common ration was found by dividing the first term by the next term