Answer:
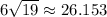 inches.
inches.
Explanation:
The longest line segment in a right rectangular prism is the diagonal that connects two opposite vertices. On the first diagram attached, the green line segment connecting A and G is one such diagonals. The goal is to find the length of segment
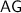 .
.
In this diagram (not to scale,)
 (length of prism,)
(length of prism,)
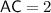 (width of prism,)
(width of prism,)
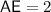 (height of prism.)
(height of prism.)
Pythagorean Theorem can help find the length of
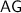 , one of the longest line segments in this prism. However, note that this theorem is intended for right triangles in 2D, not the diagonal in a 3D prism. The workaround is to simply apply this theorem on two different right triangles.
, one of the longest line segments in this prism. However, note that this theorem is intended for right triangles in 2D, not the diagonal in a 3D prism. The workaround is to simply apply this theorem on two different right triangles.
Start by finding the length of line segment
 . That's the black dotted line in the diagram. In right triangle
. That's the black dotted line in the diagram. In right triangle
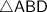 (second diagram,)
(second diagram,)
- Segment
 is the hypotenuse.
is the hypotenuse. - One of the legs of
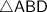 is
is
 . The length of
. The length of
 is
is
 , same as the length of this prism.
, same as the length of this prism. - Segment
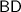 is the other leg of this triangle. The length of
is the other leg of this triangle. The length of
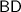 is
is
 , same as the width of this prism.
, same as the width of this prism.
Apply the Pythagorean Theorem to right triangle
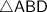 to find the length of
to find the length of
 , the hypotenuse of this triangle:
, the hypotenuse of this triangle:
 .
.
Consider right triangle
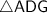 (third diagram.) In this triangle,
(third diagram.) In this triangle,
- Segment
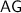 is the hypotenuse, while
is the hypotenuse, while
 and
and
 are the two legs.
are the two legs.
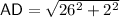 . The length of segment
. The length of segment
 is the same as the height of the rectangular prism,
is the same as the height of the rectangular prism,
 (inches.) Apply the Pythagorean Theorem to right triangle
(inches.) Apply the Pythagorean Theorem to right triangle
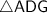 to find the length of the hypotenuse
to find the length of the hypotenuse
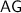 :
:
 .
.
Hence, the length of the longest line segment in this prism is
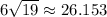 inches.
inches.