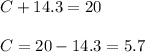Answer:
14.3€
Explanation:
Let:
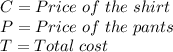
Now, let's write the data provided by the problem, using algebraic notation.
The total cost of the clothes is 20€, so:
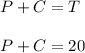
The price of the shirt is :
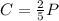
Replacing this value into the first equation:
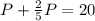
Solving for P:
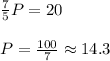
So, the price of the pants is 14.3€ and the price of the shirt is:
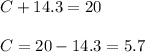
Translation:
Deja que:
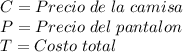
Ahora, escribamos los datos proporcionados por el problema, usando notación algebraica.
El costo total de la ropa es de 20 €, entonces:
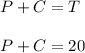
El precio de la camisa es:
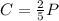
Reemplazando este valor en la primera ecuación:
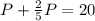
Resolviendo para P:
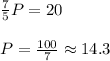
Entonces, el precio del pantalón es de 14.3 € y el precio de la camisa es: