Question

Factor the polynomial 12c9 + 28c7. Find the GCF of 12c9 and 28c7. 4c7 Write each term as a product, where one factor is the GCF. 4c7(3c2) + 4c7(7) Use the distributive property.

Answer 1

We have been given a polynomial
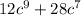`12c^9+28c^7`. We are asked to factor the given polynomial.

First of all, we will find the greatest common factor of both terms.

GCF of
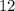`12` and
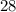`28` is 4 as 3 times 4 is 12 and 7 times 4 is 28.

GCF of
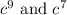`c^9\text{ and }c^7` is
`c^7`.

So GCF of
`12c^9\text{ and }28c^7` is
`4c^7`.

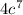Now we will rewrite each term as product of GCF and a term as:

`12c^9=4c^7(3c^2)`

`28c^7=4c^7(7)`

`4c^7(3c^2)+4c^7(7)`

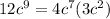
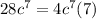
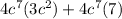
Now we will factor out
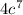`4c^7` from both terms as:

`4c^7(3c^2+7)`

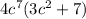
Therefore, factored form of our given expression would be
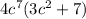`4c^7(3c^2+7)`.