Answer:
The fossil is 17,100 years old.
Step-by-step explanation:
The decay equation:
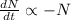
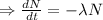
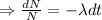
Integrating both sides
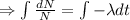
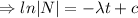
When t=0, N=
 = initial amount
= initial amount

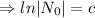
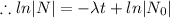
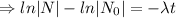
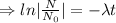
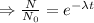
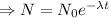
The decay equation is

Given that,
The half life of carbon - 14 is 5700 years.
For half life,

To find the value of
 , we need to put the value of N and t in the decay equation.
, we need to put the value of N and t in the decay equation.

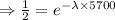 [ Divided
[ Divided
 both sides]
both sides]
Taking ln both sides
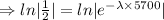

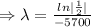
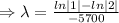 [
[
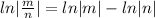 ]
]
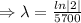 [ln 1= 0]
[ln 1= 0]
The fossil has only 12.5% of the carbon carbon-14 that it would have had originally.
So,
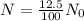
Then,
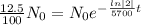
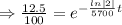
Taking ln both sides
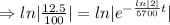
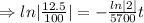
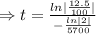
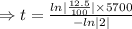
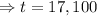
The fossil is 17,100 years old.