Given:
It is given that,
PQ ⊥ PS and
∠QPR = 7x-9
∠RPS = 4x+22
To find the value of ∠QPR.
Formula
As per the given problem PR lies between PQ and PS,
So,
∠QPR+∠RPS = 90°
Now,
Putting the values of ∠RPS and ∠QPR we get,
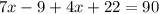
or,

or,

or,

or,
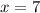
Substituting the value of
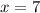 in ∠QPR we get,
in ∠QPR we get,
∠QPR =

or, ∠QPR =

Hence,
The value of ∠QPR is 40°.