Question

The admission fee at an amusement park is $1.50 for children and $4 for adults. On a certain day 333 people enter the park, the admission fee collected totaled $862. How many children and how many adults were admitted?

Answer 1

188 children and 145 adults were admitted in the park.

Explanation:

Given:

The admission fee at an amusement park is $1.50 for children and $4 for adults.

Total $862 collected on a certain day when 333 people enter the park.

Now, to find the children and adults admitted in the park.

Let the number of children admitted be
`x.`

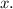
And the the number of adults admitted be
`y.`

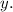
So, the total people enter the park:

`x+y=333\\\\x=333-y\ \ \ ...(1)`

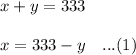
Thus, the total amount collected of the admission fee:

`1.50(x)+4(y)=862\\\\`

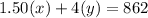
Substituting the value of
`x` from equation (1):

`1.50(333-y)+4(y)=862\\\\499.50-1.50y+4y=862\\\\499.50+2.50y=862\\\\Subtracting\ both\ sides\ by\ 499.50\ we\ get:\\\\2.50y=362.50\\\\Dividing\ both\ sides\ by\ 2.50\ we\ get:\\\\y=145.`

Thus, the number of adults = 145.

Now, to get the number of children by substituting the value of
`y` in equation (1) we get:

`x=333-y\\\\x=333-145\\\\x=188.`

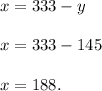
Hence, the number of children = 188.

Therefore, 188 children and 145 adults were admitted in the park.