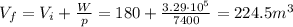Question

A cell contains 180 m^3 of gas at 7400 Pa and a machine. The machine is turned on remotely and expands the box. During this process, the machine also gives off 260 kJ of heat to the gas, and the internal energy is determined to be -69kJ. What is the final volume of the cell? Assume pressure stays constant.

Please Show All Work

Answer 1

`224.5 m^3`

Step-by-step explanation:

By using the first law of thermodynamics, we can find the work done by the gas:

`\Delta U=Q-W`

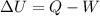
where in this problem:

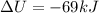`\Delta U=-69 kJ` is the change in internal energy of the gas

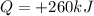`Q=+260 kJ` is the heat absorbed by the gas

W is the work done by the gas (positive if done by the gas, negative otherwise)

Therefore, solving for W,

`W=Q-\Delta U=+260-(-69)=+329 kJ = +3.29\cdot 10^5 J`

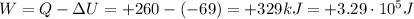
So, the gas has done positive work: it means it is expanding.

Then we can rewrite the work done by the gas as

`W=p(V_f-V_i)`

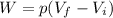
where:

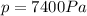`p=7400 Pa` is the pressure of the gas

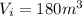`V_i=180 m^3` is the initial volume of the gas

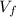`V_f` is the final volume

And solving for Vf, we find

`V_f=V_i+(W)/(p)=180+(3.29\cdot 10^5)/(7400)=224.5 m^3`