We have been given that the of a virus through a city is modeled by the function
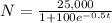 , where N is the number of people infected by the virus after t days. We are asked to find the number of days it will take for 1,500 people in this city to be infected with the virus.
, where N is the number of people infected by the virus after t days. We are asked to find the number of days it will take for 1,500 people in this city to be infected with the virus.
To solve our given problem, we will substitute
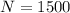 in our given equation and solve for t.
in our given equation and solve for t.
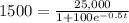
Multiply both sides by
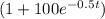 .
.
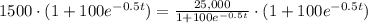
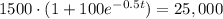
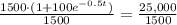
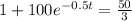
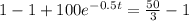
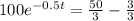
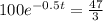
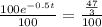
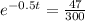
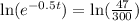
Using natural log property
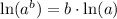 , we will get:
, we will get:
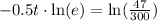
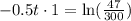
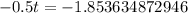
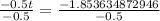
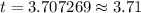
Therefore, it will take approximately 3.71 days for 1,500 people in this city to be infected with the virus.