Question

On January 1, 2010, Lucita bought a car for $25,000. If the car depreciates at a rate of 15% per year, which equation can be used to find the value of the car on January 1, 2018?

Answer 1

A

Explanation:

a1=25000(0.85)^ 9-1

The guy above is right. I just wanted to simplify the answer.

Answer 2

`a_9=25,00(0.85)^(9-1)`

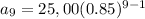
Explanation:

Let
`a_1=25,000`

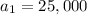
After one year, in 2001, the price is $a_2$, where

$a_2= a_1-a_1\times (0.15)$

$\therefore a_2=a_1(1-0.15)=a_0(0.85)$

Now after two years, in 2002, let the price be $a_3$

The pattern is pretty clear. After $n$ years, in $200n$ the price will be:

$a_n= a_0(0.85)^{n-1}$