Answer:
Minimum number of pennies = 10
Explanation:
Given:
Maximum number of coins Hannah have = 25
Total number of of nickels (coins) she has = 11
Total value of the combined coins = $ 0.65
We have to find the minimum number of pennies.
Let the number of pennies be "p" and no. of nickels be "n".
Note:
Value of 1 penny = $ 0.01
Value of 1 nickel = $ 0.05
Arranging the above situation in terms of equations:
According to their quantities.
⇒
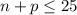 and
and
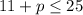 so
so
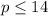
According to their values.
⇒

⇒
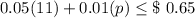
⇒

⇒
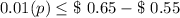
⇒
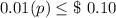
⇒
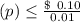
⇒

Minimum number of pennies :
⇒
 which also satisfies
which also satisfies
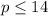
Therefore :
⇒
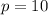
Plugging p= 10 we can verify the values.
⇒
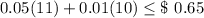
⇒
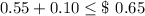
⇒

So,
Minimum number of pennies Hannah have = 10