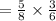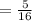Question

A box contains three plain pencils and 5 pens. A second box contains three colored pencils and three crayons. One item from each box is chosen at random. What is the probability that a pen from the first box and a crayon form the second box are selected?

Answer 1

Therefore the probability that a pen from the first box and a crayon from the second box are selected is
`\frac5{16}`

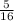
Explanation:

Probability:

The ratio of the number of favorable outcomes to the number all possible outcomes of the event.

`Probability=\frac{\textrm{The number favorable outcomes}}{\textrm{The number all possible}}`

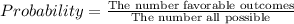
Given that,

Three plain pencils and 5 pens are contained by the first box.

Total number of pens and pencils is =(3+5)=8

The probability that a pen is selected from the first box is

=P(A)

`=\frac{\textrm{The number pens}}{\textrm{Total number of pens and pencils}}`

`=(5)/(8)`

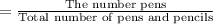
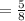
A second box contains three colored pencils and three crayons.

Total number of pencils and crayons is =(3+3)=6

The probability that a crayon is selected from the second box is

=P(B)

`=\frac{\textrm{The number of crayon}}{\textrm{Total number of crayons and pencils}}`

`=(3)/(6)`

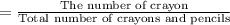
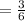
Since both events are mutually independent.

The required probability is multiple of the events

Therefore the required probability is

`=\frac58* \frac36`

`=\frac5{16}`