Question

For a trip, one high school rented and filled 5 vans and 3 buses with 114 students. Another high school instead fit its 247 students into 7 vans and 8 buses. With each bus and van seating the same number of students, how many students could a bus carry? How many students could a van carry?

Answer 1

Therefore a bus could carry 23 number of students and a van could carry 9 number of students.

Explanation:

Assume a van and a bus could carry x and y number of students respectively.

Given that,

For a trip, one high school rented and fits 114 students into 5 van and 3 buses.

So,

A van could carry x number of students

5 van could carry 5x number of students.

A buses van could carry y number of students.

3 buses van could carry 3y number of students.

∴5x+3y=114 ....(1)

Another high school instead fit its 247 students into 7 vans and 8 buses.

A van could carry x number of students

7 van could carry 7x number of students.

A buses van could carry y number of students.

8 buses van could carry 8y number of students.

∴7x+8y=247 ....(2)

∴5x+3y=114 ....(1)

and

7x+8y=247 ....(2)

7 times of equation (1) subtracts from 5 times of equation (2)

35x + 40y = 1235

35x + 21y = 798

- - -

________________

40y-21y=1235-798

⇒19y=437

`\Rightarrow y=(437)/(19)`

`\Rightarrow y=23`

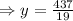
Putting the value y in equation (1)

5x+3.23=114

⇒5x=114-69

⇒5x=45

`\Rightarrow x=(45)/(5)`

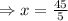
⇒ x=9

Therefore a bus could carry 23 number of students and a van could carry 9 number of students.