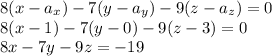Question

Steve Herr is an architect in Minneapolis, Minnesota. His latest project is designing a park. On the blueprint, the park is determined by a plane which contains the points at (1,0,3), (2,5,0), and (3,1,4) One of the features of the park is a monument that must be perpendicular to the ground. Find a nonzero vector, representing the monument, perpendicular to the plane defined by the given points.

Answer 1

A on Edge 2020

Explanation:

Answer 2

8i - 7j - 9k

Explanation:

We have three points:

A (1,0,3)

B (2,5,0)

C (3,1,4)

First of all, we write the following two vectors:

`AB=(2-1,5-0,0-3)=(1,5,-3)`

`BC=(3-2,1-5,4-0)=(1,-4,4)`

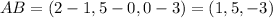
These two vectors connect A with B and B with C, and since these 3 points lie on the plane, the two vectors also lie on the plane.

Therefore, the cross product of these two vectors must be a vector perpendicular to the plane.

The cross product of the two vectors is:

`AB * BC = i(5\cdot 4 -(-3\cdot-4))+j(-3\cdot 1 -1\cdot 4)+k(1\cdot -4-5\cdot 1)=\\=8i-7j-9k`

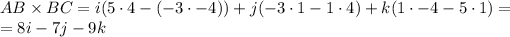
And the equation of the plane can be found as:

`8(x-a_x)-7(y-a_y)-9(z-a_z)=0\\8(x-1)-7(y-0)-9(z-3)=0\\8x-7y-9z=-19`