Question

Need help on 3/4 please help me fast please read it and help me !!!!!!!!!fast!!!!!!!

Answer 1

Explanation:

3) ΔABC ≅ ΔDEF

AB = ED {Corresponding parts of corresponding triangles are equal}

6y - 4 = 4y +2

add 4 to both sides

6y - 4 + 4 = 4y + 2 + 4

6y = 4y + 6

subtract 4y from both sides

6y - 4y = 4y + 6 - 4y

2y = 6

Divide by 2

`(2y)/(2)=(6)/(2)\\`

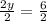
y = 3

AB = 6y - 4 = 6*3 - 4 = 18 - 4 =14

AB = 14

ΔABC ≅ ΔDEF

∠A = ∠D {Corresponding parts of corresponding triangles are equal}

5x + 2 =87

5x = 87 - 2

5x = 85

x = 85/5

x = 17

In ΔDEF,

∠D + ∠E + ∠F = 180° {SUM OF ALL ANGLES OF TRIANGLES}

87 + 42 + ∠F = 180

129 + ∠F = 180°

∠F = 180 - 129

∠F = 51°

ΔABC ≅ ΔDEF

∠C = ∠F {Corresponding parts of corresponding triangles are equal}

3y = 51

y= 51/3

y = 17