Answer:
Therefore the value of bond will triple after 17.72 years.
Explanation:
The formula of Compounded continuously
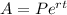
A= Amount after t year
P= initial amount
r = rate of interest
t= time in year.
Given that,
Jacobs college saving are invested in bond that pay 6.2% compounded continuously.
Let after t years the initial amount P will be triple i.e 3P.
Here P=P, A=3P, r= 6.2%=0.062
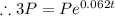
 [ Multiply
[ Multiply
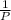 both sides]
both sides]
Taking ln both sides
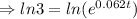
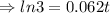 [ since
[ since
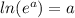 ]
]
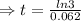
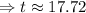 years
years
Therefore the value of bond will triple after 17.72 years.