Question

A fast-food restaurant claims that a small order of french fries contains 120 calories. A nutritionist is concerned that the true average calorie count is higher than that. The nutritionist randomly selects 35 small orders of french fries and determines their calories. The resulting sample mean is 155.6 calories, and the p-value for the hypothesis test is 0.00093. Which of the following is a correct interpretation of the p-value?

a. If the population mean is 120 calories, the p -value of 0.00093 is the probability of observing a sample mean of 155.6 calories or less.
b. If the population mean is 120 calories, the p-value of 0.00093 is the probability of observing a sample mean of 155.6 calories or more, or a sample mean of 84.4 calories or less.
c. If the population mean is 155.6 calories, the p-value of 0.00093 is the probability of observing a sample mean of 120 calories or more.
d. If the population mean is 155.6 calories, the p-value of 0.00093 is the probability of observing a sample mean of 120 calories or less.

Answer 1

A

Explanation:

If the population mean is 120 calories, the p-value of 0.00093 is the probability of observing a sample mean of 155.6 calories or more.

Answer 2

Correct option is (C).

Explanation:

The p-value is well defined as the probability, [under the null-hypothesis (H₀)], of attaining a result, of a statistical hypothesis test, equivalent to or greater than what was the truly observed.

A small p-value (typically ≤ 0.05) specifies solid proof against the null hypothesis (H₀), so you reject the null hypothesis.

A large p-value (> 0.05) specifies fragile proof against the H₀, so you fail to reject the null hypothesis.

A nutritionist is concerned that the true average calorie count in the french fries served by a fast-food restaurant is higher than 120 calories.

The hypothesis to test this can be defined as:

H₀: The true average calorie count in the french fries is 120 calories, i.e. μ = 120.

Hₐ: The true average calorie count in the french fries is more than 120 calories, i.e. μ > 120.

The test statistic is:

`z=(\bar x-\mu)/(\sigma/√(n))`

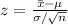
The sample mean calories in the sample of 35 small orders of french fries is,

`\bar x=155.6`

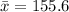
And the p-value is,

p-value = 0.00093

The p-value can be interpreted as the probability of getting a sample of 155.6 calories or greater when the population mean is 120 calories.

That is,

`\bar x-\mu=155.6-120=35.6`

The p-value can also be interpreted as probability of getting a sample of 84.4 calories or less when the population mean is 120 calories.

`\bar x-\mu=-35.6`*

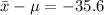*Since the normal distribution is symmetric the P (Z < -z) = P (Z > z).

So,

`\bar x-\mu=-35.6`

`\\\bar x=-35.6+120\\\bar x=84.4`

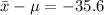
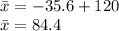
Thus, the correct option is (C).