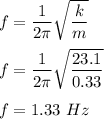Question

A 50-cm-long spring is suspended from the ceiling. A 330g mass is connected to the end and held at rest with the spring unstretched. The mass is released and falls, stretching the spring by 28cm before coming to rest at its lowest point. It then continues to oscillate vertically.

A. What is the spring constant?

B. What is the amplitude of the oscillation?

C. What is the frequency of the oscillation?

Answer 1

Step-by-step explanation:

Given that,

Length of the spring, l = 50 cm

Mass, m = 330 g = 0.33 kg

(A) The mass is released and falls, stretching the spring by 28 cm before coming to rest at its lowest point. On applying second law of Newton at 14 cm below the lowest point we get :

`kx=mg\\\\k=(mg)/(x)\\\\k=(0.33* 9.8)/(0.14)\\\\k=23.1\ N/m`

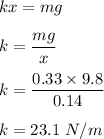
(B) The amplitude of the oscillation is half of the total distance covered. So, amplitude is 14 cm.

(C) The frequency of the oscillation is given by :

`f=(1)/(2\pi)\sqrt{(k)/(m)} \\\\f=(1)/(2\pi)\sqrt{(23.1)/(0.33)} \\\\f=1.33\ Hz`