Question

An industrial engineer is planning to test the claim that the mean cycle time of a particular assembly process is less than 10 minutes. She sets α = 0.05 and plans to take a SRS of 100 such processes and record the cycle time for each. If the true mean cycle time of the assembly process is 9.78 minutes the power of her test is 0.85. In all possible samples of size 100 she will:

Answer 1

Make a Type I error 15% of the time.

Explanation:

The question is incomplete:

In all possible samples of size 100 she will:

1. Make a Type II error 5% of the time
2. Reject the null hypothesis 15% of the time
3. Make a Type I error 5% of the time
4. Fail to reject the null hypothesis 85% of the time

Option 2 and 4 are both false because we can not estimate this probabilitites a priori.

Option 1.

The power of a test is defined as the conditional probability of rejecting the null hypothesis, given that the alternative hypothesis is true.

Then, the power of the test is complementary of the probability of failing to reject the null hypothesis, gicen that the alternative hypothesis is true. The last is the definition of the probability of a Type II error.

This means that a power of 0.85 implies a probability of (1-0.85)=0.15 of making a Type II error.

`P(Type \,II\, error)=1-Power=1-0.85=0.15`

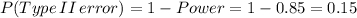
The option 1 ("Make a Type II error 5% of the time") is not precise, so it is not correct.

Option 3

The significance level is 0.05. This is also the probability of making a Type I error.

The option 3 ("Make a Type I error 5% of the time") is correct.