Question

When records were first kept (t=0), the population of a rural town was 260 people. During the following years, the population grew at a rate of P'(t) = 45(1+sqrt(t)).

a) what is the population after 15 years?
b) find the popuation P(t) at any time t > 0.

Answer 1

(a) The population after 15 years is 2678.

(b)Therefore the population P(t) at any time t>0 is

`P(t)= 45t+30 {t^(\frac32)}+260`

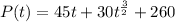
Explanation:

Given that,

The population grew at a rate of

`P'(t)=45(1+\sqrt t)`

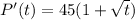
Integrating both sides

`\int P'(t) dt=\int 45(1+\sqrt t)dt`

`\Rightarrow \int P'(t) dt=\int (45+45\sqrt t)dt`

`\Rightarrow \int P'(t) dt=\int 45\ dt+\int 45\sqrt t\ dt`

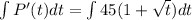
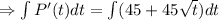
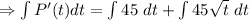
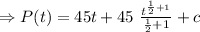`\Rightarrow P(t)= 45t+45\ (t^(\frac12+1))/(\frac12+1)+c` [ c is integration constant]

`\Rightarrow P(t)= 45t+45\ (t^(\frac32))/(\frac32)+c`

`\Rightarrow P(t)= 45t+45*\frac 23 * {t^(\frac32)}+c`

`\Rightarrow P(t)= 45t+30 {t^(\frac32)}+c`

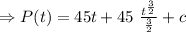
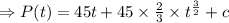
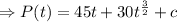
When t=0 , P(0)= 260

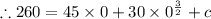
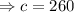
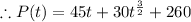
`\therefore 260= 45*0+30* {0^(\frac32)}+c`

`\Rightarrow c=260`

`\therefore P(t)= 45t+30 {t^(\frac32)}+260`

Therefore the population P(t) at any time t>0 is

`P(t)= 45t+30 {t^(\frac32)}+260`

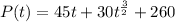
To find the population after 15 years, we need to plug t=15 in the above expression.

`P(15)=( 45* 15)+30( {15^(\frac32)})+260`

≈2678

The population after 15 years is 2678.